The Influence Of Quantum Mechanics On Philosophy
“When Henry Sidgwick casually remarked in a letter that as he grew older his interest in what or who made the world was altered into interest in what kind of a world it is anyway, his voicing of a common experience of our own day illustrates also the nature of that intellectual transformation effected by the Darwinian logic.”
John Dewey, “Influence of Darwinism In Philosophy”
I suppose it best to start at the beginning: the title. This little piece is titled after John Dewey’s “Influence Of Darwinism In Philosophy”, which conveniently also begins its analysis with the title of Darwin’s book.
The very word “species”, as Dewey notes, comes from the Latin verb “specio” (to look) and the stem “ies” which converts a verb into an abstract noun. The word is a Romanization of the central Greek concept of “ἰδέα”. “Ιδέα” is not just a word, it’s a phoneme that encompasses an entire world view built into all of western thought at its very foundation. How long before Darwin it had been the goal of philosophers to escape the world of ἰδέα is shown by this: Aristotle himself declares that escape is his goal in both Logic and De Anima. Careful philologist/philosophers such as Paul Shorey (Roosevelt Lectures) and D’Arcy Wentworth Thompson (Excess And Defect) have amply demonstrated Aristotle’s failures. Darwin himself gives another example of Aristotle’s failure in his “Historical Introduction” to Origin Of Species.
The goal of this piece is indicated by the title: I submit to see how quantum mechanics has influenced philosophy, as Dewey submitted to see Darwinism. But there the title play stops, for reasoning from the words in the title “Quantum Mechanics” bears poor fruit. The word “quantum” is also Latin, meaning “how much”. Cicero says that the good and the wicked are never close friends for “nisi quod tanta est inter eos, quanta maxima potest esse, morum studiorumque distantia.”. Mechanics comes from the Greek μηχανή, meaning device or method. There is a history to these words. The term “mechanics” for the abstract dynamics comes from the Victorian belief that abstract dynamics would provide a way of describing apparently qualitative change as the quantitative change of state of what were ultimately very small machines. But this is not a philosophical history - or at least the argument that it is would take up an entire post in its own right. Dewey’s use of the title is illustrative rather than essential. The point is that philosophy and physics share concepts:
“Wo sich ein Körper bewegt, da ist Raum und Zeit, das simpelste empfindende Geschöpf in dieser Welt wäre also das Winkel und Zeiten messende. Unser Hören und vielleicht auch unser Sehen besteht schon in einem Zählen von Schwingungen.
Lichtenberg, Sudelbücher: D
Dewey illustrates that science and philosophy share not only concepts but also aesthetics – senses of beauty. Traditional philosophy and science had held that the most beautiful and complete explanation was the explanation from ultimate origin to ultimate end. Even the motion of a pendulum was, as Kuhn put it, an “infinitely complicated” problem. The explanation of the pendulum started with its conception and design, passed through an infinite series of faster and smaller beats and ended with its conceptual transition from a moving object to a stationary object. Galileo’s revolution was to reconceptualize the pendulum as a system described in three numbers - radius, amplitude and frequency. As the pendulum users refined Galileo’s theory, the debate shifted, but the revolution remained. What the users want is for the system to be described simply by the theory, not to be given a conceptual path from ultimate conception to ultimate end. This change in aesthetic has become more permanent as classical pendulum theories have been left behind.
Most people agree that what is now called classical mechanics has had enormous philosophical impact, but many would deny this role for quantum mechanics. Perhaps this is for historical reasons: the scientific issues which confronted western philosophy (ignoring the Athenian Greek period) just before the industrial revolution put the scientific issues at the core of human society were issues within the world of classical mechanics. Philosophical conversations about “determinism” and mechanism are often conducted in oddly classical registers even today. Quantum processes are more vital to our lives than classical mechanics was to the industrial revolution, but scientific issues can be put at the core of a philosophy but once.
The example I often return to as an illustration of the doing of quantum mechanics is ammonia synthesis, the industrial chemical process which produces the fixed nitrogen necessary to continue human life on earth. Quantum mechanics links the chemical composition of the chemicals under examination to the spectra produced when heated by x-rays. Examining these spectra allows one to develop an extremely detailed analysis of the dynamics involved.
Despite the extreme importance of quantum mechanics, I don’t pretend it is uniquely important. One could write a great essay about the influence of, say, fluid mechanics on philosophy. Hopefully CVAR will have such an essay one day soon. The main benefit of choosing quantum mechanics is pedagogical: enormously many people (everyone who has taken an intro to chemistry course for instance) have used quantum mechanics but not nearly as many people do quantum mechanics. Many people have this nagging feeling that they know something important about atoms but can’t quite explain anything about it. They know that quantum mechanics should influence ideas of space, time, measure, etc. but are not quite sure how it does so.
This use/do distinction is universal. Even Niels Bohr was careful to title his books like “The Theory of Spectra and Atomic Constitution”, “Atomic Physics And The Description Of Nature”, and (my favorite) “The Penetration Of Charged Particles Through Matter”. These titles emphasize the using of quantum mechanics.
Perhaps, as a society, we are in a similar situation to Socrates’ contemporaries or Leibniz’s contemporaries in our relationship with our scientific visions. To make the meaning of this implausible assertion concrete, I will look at three areas in which quantum mechanics has (or should have) fundamentally altered our philosophical conceptions. As a prophylactic against mysticism, I will not go into traditional “philosophy of quantum mechanics” subjects like measurement. Instead our subjects are simpler and more experimentally grounded concepts like the identity between creation and motion and the pluralization of determinism.
Identity Between Creation And Motion
“Ce principe [de raison suffisante] posé, la première question qu’on a droit de faire sera : Pourquoi il y a plutôt quelque chose que rien ? Car le rien est plus simple et plus facile que quelque chose. De plus, supposé que des choses doivent exister, il faut qu’on puisse rendre raison pourquoi elles doivent exister ainsi, et non autrement. ”
Why is there something rather than nothing - surely few questions can be as annoyingly philosophical than this. Leibniz moves too quickly, but his next sentence contains the only solution actually available to ordinary physics: everything that exists is a little miracle. Nothing new can come into being, there is only transformation - as Leibniz puts it “Il n’y a donc point de métempsycose, mais il y a métamorphose”.
To talk a little shop, we can talk about this in classical mechanics terms. Physicists are used to relating the “dimension” (number of unknowns) of a classical mechanics problem to the number of particles. For example, the number of dimensions of a one component system where each molecule has no internal degrees of freedom (rotations, vibrations, etc) should be 6 times the number of molecules - three for each position, and three for each momentum. Now, we mathematicians have elaborately proven that dimension is an invariant under continuous transformation. In practice, this means no continuous motion can ever create or eliminate a molecule, including the actual physical motion as a special case.
The idea of the preservation of matter has been very powerful. For Arthur Eddington, the first to propose that stars are powered by nuclear fusion, the matter was so settled that the trick was not to show how each miraculous little proton was necessary but to count even count them to a unit:
“I believe there are 15, 747, 724, 136, 275, 002, 577, 605, 653, 961, 181, 555, 468, 044, 717, 914, 527, 116, 709, 366, 231, 425, 076, 185, 631, 031, 296 protons in the universe and the same number of electrons.”
Yet it was Eddington’s own scientific field - the quantum mechanics of the atomic nucleus - that fundamentally altered the question.
Perhaps a little historical narrative and a focus on experiments over theory will clear things up. All radioactivity experiments from Marie Curie to Ernest Rutherford had found exactly four components of the atomic nucleus, each of which turned out to be known physical objects. In order from least to most penetrative of matter, these components are:
A larger positively charged “alpha” particle
A much, much smaller and negatively charged “beta” particle
and the uncharged and electrically neutral “gamma” particle
These particles had a range of apparently mysterious properties. The alpha particle has ~4 times the mass of the hydrogen ion and only twice the charge. The sole possible explanation in terms of already observed particles: the atomic nucleus was made of bound hydrogen ions and beta particles. The positive charge on the nucleus is the excess of hydrogen ions over beta particles. If one didn’t think about it too hard, it made sense: there was a mysterious nuclear force binding a hydrogen ion to a beta particle more tightly than the electrostatic force holding together neutral hydrogen. Even the conditions under which alpha and beta coalesce into a neutral particle can be guessed at: the other Charles Darwin had shown under certain relativistic conditions, these particles must coalesce. These conditions are hard to attain, in line with the rarity of elemental change.
The resulting picture of the nucleus is a bit disturbing. Even the helium nucleus consists of two hydrogen ions and an H2 molecule confined into a distance comparable with the scattering length of one free electron. In other words, there seemed to be a proper part of most atomic nuclei which had the parts of four hydrogen atoms squeezed into less than 100,000th the size of a hydrogen atom.
Further experimental facts only make the picture more disturbing. As noted above, beta radiation was distinguished from alpha by its highly penetrative character. Yet the bound electrons refuse to escape the tiny radius of the nucleus!
So far I have been careful not to actually raise the issue of quantum mechanics, only experimental facts. As these experimental facts piled up, quantum mechanics brought the issues of the proton-electron picture to the level of a contradiction. The so-called Klein Paradox means that an extremely steep potential cannot trap an electron. The Klein Paradox means that if the energy for an electron to escape a well (modeled as a step function for simplicity's sake) is greater than the sum of the kinetic and rest energy of the electron then there must be a positive transmission probability. This is a result of the same relativistic symmetries that make antimatter necessary: in order for a reflection to be possible - that is, a solution where the electron reverses its velocity at the barrier - there must also be a refraction solution - that is, a solution where the electron keeps its velocity but reverses its momentum at the barrier. An electron would be freed, not bound by a strong enough potential.
But then, if all this is the case, whence all the electrons? The simplest conclusion is that the electrons are not in there at all - but then why do they fly out during beta decay. Bohr proposed that the electrons are created by the process of beta decay. The creation of a particle is thus a part of the motion of the system no more privileged than any other motion. This is a proposal that makes sense only in the light of quantum mechanics, where the quantum numbers, such as electron number, are the most fundamental considerations.
The existence of an electron - the number - is simply quantized motion, rather than being a little miracle like the existence of a classical particle. But from whence electrons at all? And how did they get there?
There’s a traditional quantum mechanics approach to understanding the existence of objects that goes back to Bohr called “building up” or “aufbauen”. If an aufbauen approach, one imagines that the object of interest is made up one piece at a time, and proceeds by asking why that subobject is stable. Since quantum particles do not have a history (no hair as some say), an atom built using this method is fully general.
The aufbauen approach is the modern interpretation of Leibniz’s method, outlined above, and is a great approach for answering why there are atoms and other compound objects. Thus it explains everything physical that Leibniz would want to explain. But what about simples such as electrons? Can we go beyond even Leibniz’s wildest goals?
Quantum theory rephrases the question of creation of simples from the total miracle that happens once and for all time – as it was in classical theory – to a mini miracle that may or may not be happening at any time, all the time. Because the particle creation operator in quantum mechanics is not an observable we cannot go beyond “may or may not”. The unobservability of particle creation is a necessary feature of the correspondence principle that is formalized by modern quantum mechanics.
The nonobservability of particle creation is the quantum correspondent to the classical mystery of creation. Perhaps there is more to say, but once we try to get into “explaining non observable phenomena” we are well outside the experimentally verified quantum mechanics that is the purview of this column.
The Pluralization Of Determinism
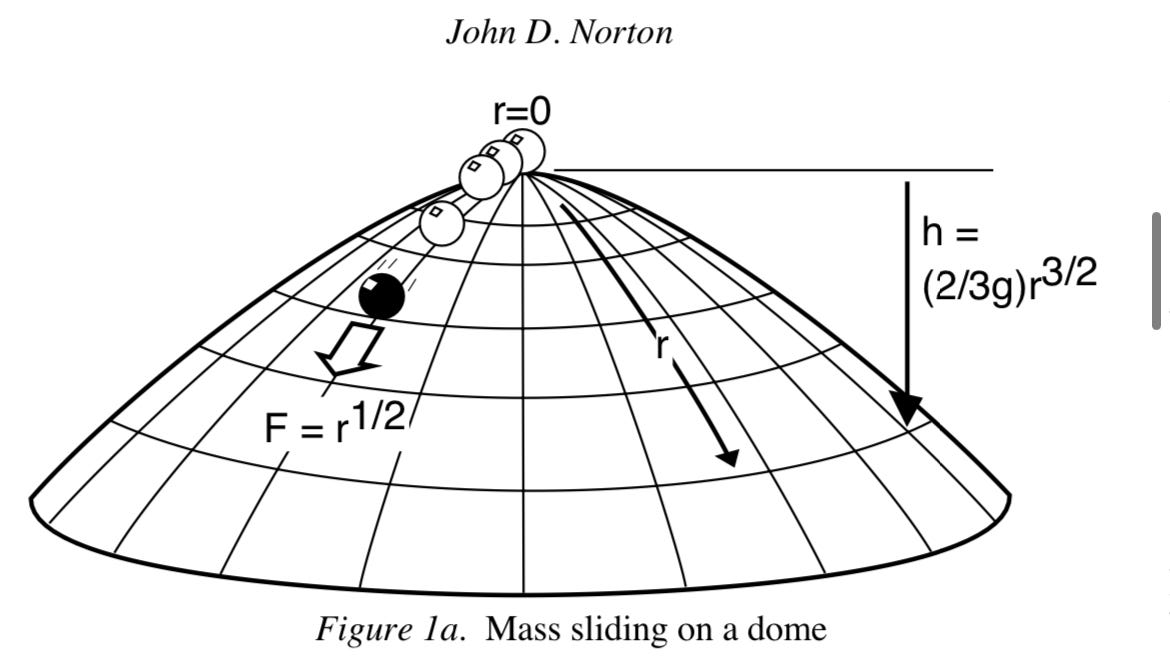
Quantum mechanics teaches that creation is a form of motion, but what can be said of motion itself? From Plato and Democritus we have often been told that all change is motion, so the science of motion becomes science tout court. Similarly, determinism has been a requirement of science for a long time: Aristotle criticized the Atomists for their indeterminism. Contrariwise, many modern philosophers - Bertrand Russell, John D Norton - have criticized the concept of a single all encompassing causal relation as a pre scientific idea. If you like, you can dismiss the whole “free will vs determinism” argument as one kind of folk ontology (vague, inchoate causes) vs another (vague, inchoate mindstuff). Now, Norton & Russell’s arguments are more general than what we need, so I will just describe one of Norton’s examples to get the flavor. I will call this example Norton’s Hill, though the idea is much older (there is a generic variant on Wikipedia).
Figure 1a from “Causation As Folk Science” by John Norton. I’m calling this “Norton’s Hill”.
Imagine that you’re placing a very small hot wheels toy car on the hill and flicking the car with your finger. Consider the relation between a pair of points on the hill and the possible times it can take to get between those points. Generally the range of times to get from point a to point b will be a large set, because if you have one nice path from a to b that doesn’t go over the peak, then you can try to move the initial angle a little closer to the peak and raise the initial kinetic energy slightly to hit the same point on the downslide.
If points a and b and the peak of Norton’s Hill are in line with point a closer to the peak than point b, then that correspondence has a range with no minimum. One can always get from point a to point b faster by pointing your hot wheel at point b and flicking it harder.
But is there a maximum time to get from point a to point b? If one points your hot wheel at the peak of the hill, then one gets a significantly longer time of transit. Consider a sequence of paths getting closer and closer to the peak before turning around. In order to slide back down to point b, the energy has to decrease as one gets closer to the peak. There are two competing considerations: the infinite slow down as one approaches the peak and the smaller and smaller distance traveled one gains in each adjustment. Since the time is the ratio of distance to velocity, the outcome depends on the limit of this ratio. Norton chose the slope of the hill so that one can reach the peak at zero velocity at finite time from any point. By symmetry, the amount of time to reach point b should be twice the amount of time to roll to the peak at zero final velocity from point minus the time spent between b & a.
This value seems to be the maximum… but the solution makes no sense. At the peak of the hill one has no momentum and no force (the peak of the hill is flat). Why would the hot wheel start rolling down hill? Much more reasonable to say that the hot wheel rolls uphill and we sit at point b with our stopwatch iterating seconds. Morally, it should take infinite time for one to go from the peak to point b if one has zero velocity at the peak.
These two solutions, one finite and the other infinite, form the basis for the two solutions which Norton gives analytically. To connect these paragraphs to his exposition: I started with what he calls the time reversal symmetry solution and built up to the simple analytic solution.
Okay, enough of that. The point of Norton’s hill as an example (not to be confused with its peak as a location!) is to show that determinism is not a rigorous consequence of Newton’s laws. The issue is that criticizing the concept of determinism is easier than abandoning it. Bertrand Russell himself had trouble: after demolishing the vague concept of a causal relation, he invoked against free will causes far vaguer than any supposed causal relation.
Perhaps going back to the history of the problem will help. Aristotle criticized the atomists for being unable to explain the origin of motion as if he had an explanation himself. Perhaps an impulse to outdo the Aristotleans led Newton to so strongly emphasize the determinism of his system of the world (a system that included more than just his laws of motion!). Newton is careful to demonstrate that each possible solution to his orbital theories is deterministic (for instance Book I, Section VI, Proposition XXXI has the proof for elliptic orbits).
But Newton’s boasts betray his doubts. As Norton’s hill demonstrates, classical mechanics is not in general deterministic. Even in Newton’s lifetime, Leibniz had made terrific hay of the unacceptable indeterminism of the laws of impact. In modern language, Leibniz was complaining about the effects of a delta potential. Even with all this, following Newton it became common, especially in France, to assert that the “laws of physics” are themselves “deterministic” or “mechanical” - that determinism was something that did not need to be proven for each problem as Newton did but instead somehow simply followed from the fact of the structure of Newtonian mechanics.
This kind of thinking is typical of 18th/19th century French mathematics. The dimension - “number of unknowns” - of a typical problem of point particle motion is 6 times the number of molecules. That’s three unknown position coordinates and three unknown velocity coordinates at time t. The initial conditions provide 6 times the number of molecules separate equations. The dimension of the solution is the dimension of the background space minus the number of equations one is required to satisfy. Assuming everything is in general position, equation counting tells that at each moment one has a discrete collection of where to go next moment.
But this is not enough for determinism. For determinism, you need a unique next step rather than just a finite number of possible next steps. Pace the French, determinism requires analytic assumptions beyond just equation counting. You can reinterpret Norton’s hill as a disk with very small arrows pointing in the direction gravity would pull you, a so-called “vector field”. The vector field has deterministic dynamics if the arrows never cross, which happens if the force function has a derivative almost everywhere which is bounded above by a constant. The derivative of Norton’s force function blows up at the origin, which breaks determinism.
Equation counting is a siren song in the true sense: the Homeric sirens were not birds but goddesses who sang incomprehensible truths. For physics and philosophy of physics, equation counting always has a force far greater than its rational criticism. Thus is the origin of the famous Problem Of Free Will. So strong is the song of equation counting that before quantum mechanics the only notion of determinism that mattered was the notion implicit in classical mechanics. This put the philosopher at a disadvantage: good philosophy would show that mechanics is not mechanistic, but if one said in so many words that mechanics is not mechanistic one was accused of misunderstanding the concept.
There were a couple of people, of whom Charles Peirce & Henri Bergson are the most important, who did deny the notion of determinism (supposedly) implicit in classical mechanics. Russell in the piece linked above duly accused Bergson of not understanding scientific concepts.
But these men were thus indeterminists. This simple classification is no longer necessary nor possible, for now there are at least two fundamental notions of determinism: that of classical and that of quantum mechanics.
First of all, why is the concept of causality different in quantum rather than classical mechanics? The difference in causal concepts is, as Bohr showed, a necessary consequence of the famous wave-particle duality. A simple - say, spherical - particle is described by center and radius occupied at a particular time. A simple wave - say, a sine wave - is described by wavenumber, frequency and amplitude. Planck’s constant times the frequency (wavenumber) is the energy (momentum). Confinement in spacetime is natural to particles but unnatural to waves and vice versa. What classical mechanics hides is that having a particular energy/momentum is unnatural to particles. A conspiracy of waves with varying frequency/wavenumber (i.e. energy/momentum) to make a wavepacket confined in space, the spread of this conspiracy is the famous “uncertainty principle”.
To recapitulate, tying motion to spacetime location requires such a host of extra equations - the 6N equations above - constraining the possible functions from clock time to spatial location that the solution is not knife edge (1D) but knife point (0D). What we just established is that the knifepoint relation between kinematics and dynamics is Newtonian mechanics. We earlier cast doubt whether this was the intuitive ideal of “determinism”. In the era after Newton, this latter demonstration didn’t matter: determinism was the notion within the structure of Newtonian mechanics and if that wasn’t some “intuitive” idea, then so much the worse for intuition. But waving our hands at Newton’s laws and saying “determinism” is not appropriate for quantum mechanics. But then what notion is appropriate? We can look at an example related to Norton’s hill: a central potential with the form V=(2/3)(r^(3/2)).
A few facts about central potentials generally, because often much of the facts about the solution to a quantum problem can be read off the symmetries. Spherical symmetry means that Schrödinger equation for a central potential separates into a radial and an angular part. The angular part is the same for all central potentials with our boundary conditions gives us two quantum numbers: the azimuthal quantum number ℓ and the orbital quantum number m. The meaning of these numbers is: 1) the total angular momentum of the particle is a function of ℓ and 2) the angular momentum in a particular direction is proportional to m.
Perfect spherical symmetry is obviously a strong constraint on the angular aspects of a problem, but it doesn’t seem like it tells us anything about the radial aspects, which is where all the classical problem is! Okay yes, the classical problem is independent of angular momentum but we will see the quantum problem is not independent of ℓ in particular. I had to introduce those numbers. But what of the radial dependence? Here we must add boundary assumptions. Our assumptions are
That there is any localization at all (the wave function decays as r goes to infinity)
That the wave function is finite at the origin.
Independent of the shape of the potential, these already imply that
The wave function near the top of the hill has the form has the form r^ℓ.
The wave function exponentially decays far from the origin
There’s one more bit that comes from pure wave mechanics: with a localized wavefunction we expect a finite number of nodes (zeroes). There are ℓ at the origin and one at infinity, the remainder being the nodal quantum number n (not to be confused with the principal quantum number). The energy is a function of the count of nodes, n and ℓ.
Putting all this together, we expect a form something like:
r^ℓ F(r) exp(-r)
Where F is a sequence of functions that depend on n and ℓ, each with finitely many zeros. (Çiftci, Ateser and Koru, 2003) suggest approximate solutions of this form based on interpolation between two exact solutions.
So what is the philosophical result of all this? I hope that I have convinced you that the outcome of the quantum algorithm is perfectly well behaved wave functions and thus perfectly well behaved probability density functions. That is, for each triple n, ℓ and m there is a differential P(r) dr which gives the probability of being found at a radius of about r from the top of Norton’s Hill. This probability can be interpreted as an expected waiting time to detect a particle a distance r from the origin.
Come back to classical mechanics for contrast. Classical mechanics cannot answer the question of how long should I expect to wait to roll down Norton’s Hill. As soon as one reaches the peak with zero velocity, all bets are off. Maybe you’ll fall down, maybe not. This is the sense in which quantum mechanics is more deterministic than classical mechanics. It’s not the case that classical mechanics answers every question but sometimes wrongly and quantum mechanics answers few questions but always rightly, but rather that quantum mechanics and classical mechanics answer overlapping but distinct sets of questions, with the classical answer standing as an approximation to the quantum answer where the explanations overlap.
There are thus at least two fundamentally different notions of determinism in physics: the relation between dynamics and kinematics in classical physics and the well posedness of wave function in quantum mechanics.
This is our result, but again what is the philosophical implication? What one observes is that successes of the classical mechanics notion did not depend on their metaphysical “correctness” but rather that they inspired researchers to ask questions that were appropriate to classical mechanics. In the long and short, we return to Dewey. To paraphrase Quine: the considerations of which guides to choose from one’s scientific heritage to solve one’s actual problems are, where rational, pragmatic.